Paralelno RC kolo

 

 

Ako imamo paralelnu vezu aktivnog otpora i kondenzatora kapacitivnosti C i ako se kolo napaja sinusoidalnim naponom oblika:

 

 

 u kolu će se uspostaviti sinusoidalna raspodjela struje, čiji je opšti oblik:

 

                                                                              (1)

 

 

 

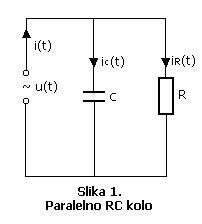
Za paralelnu vezu elemenata električnog kola karakteristično je da je na krajevima svakog elementa električnog kola isti napon, u ovom slučaju napon izvora u(t), što je prikazano na Slici 1.:

 

 

U skladu sa prvim Kirchoffovim zakonom, ukupna struja i(t) jednaka je sumu trenutnih vrijednosti struja u granama:

 

                                                                                            (2)

 

Trenutna vrijednost jačine struje koja protiče kroz otpornik se dobije kada se podijeli trenutna vrijednost napona na otporniku (koji je jednak naponu izvora, jer je riječ o čisto paralelnoj vezi!) sa vrijednošću otpornosti termogenog otpora, tj:

 

                                                                                 (3)

 

pri čemu amplituda struje predstavlja količnik maksimalne vrijednosti napona i otpora.

Struja koja protiče kroz kondenzator se može izračunati prema izrazu:

 

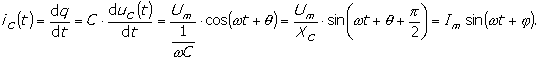                                                                                                                                    (4)

 

Uvrštavanjem u prvi Kirchoffov zakon dobijamo jednakost:

 

                                    (5)

 

Koristeći adicionu formulu za sumu dvije trigonometrijske funkcije, odnosno izraz:

 

 

 može se odrediti trenutna vrijednost struje izvora:

 

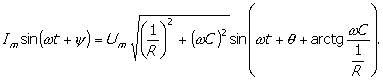                                (6)

 

 

U jednačini  (6)  moguće je definisati  slijedeće veličine:

 

- aktivna provodnost, konduktansa:

 

 

- kapacitivna (reaktivna) provodnost, kapacitivna susceptansa:

 

 

- ukupna provodnost električnog kola, admitansa kola:

 

 

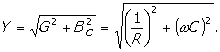
Poređenjem odgovarajućih članova sa lijeve i desne strane jednačine (6) definišu se i:

 

- maksimalna vrijednost ukupne struje u električnom kolu:

 

 

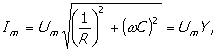
- početna faza ukupne struje u električnom kolu:

 

 

 

Trenutna snaga je izražena relacijom:

 

                                                                                                       

 

Trenutna vrijednost snage na otporniku otpornosti R je:

 

 

Trenutna vrijednost snage na kondenzatoru kapacitivnosti C je:

 

 

 

Korištenjem simboličkog metoda može se na jednostavan način izvršiti proračuna stanja u nekom električnom kolu. Ovaj metod je vrlo pogodan i za predstavljanje kompleksnih oblika ovih veličina u kompleksnoj ravni.

Primjenom simboličkog metoda na primjeru analiziranog  paralelnog RC kola dobijaju kompleksne efektivne vrijednosti napona i struje:

 

 

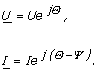
Na osnovu jednačine kontinuiteta moguće je napisati:

 

                                                                                                            (7)

 

Kako na krajevima svakog od posmatranih elemenata djeluje isti napon (u),  to se gornja relacija može predstaviti i u obliku:

 

                                                                          (8)

 

Veličina u zagradi predstavlja recipročnu vrijednost kompleksne impedanse kola, što slijedi iz poznatog Omovog zakona u kompleksnom obliku:

 

 

Dobija se:

 

 

Kako veličina  predstavlja provodnost kola, to se u skladu s vezom kompleksne impedanse i admitanse kola može pisati:

 

                                                                                 (9)

 

gdje su:

 

 

i

 

 

Iz uspostavljene veze struje kroz kolo i napona na krajevima kola može se zaključiti da karakter admitanse kola određuje iznos struje kroz kolo i njen fazni pomak u odnosu na priključeni napon. Iz

 

                                                                        (10)

 

dobija se iznos argumenta impedanse:

 

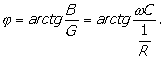                                                                                     (11)

 

Za realno električno kolo (paralelno RC kolo), prisutne su i aktivne i reaktivne komponente, te postoji i prisutnost obiju energetskih tendencija, od nepovratnog karaktera (čisto aktivno kolo) do reverzibilnog karaktera (reaktivno kolo).

 

Srednja snaga, odnosno aktivna snaga:

 

                                                                                                          (12)

 

Veličina cosφ se naziva faktorom snage, te je očigledna tendencija da ovaj faktor bude po mogućnosti jednk jedinici.

 

Reaktivna snaga koja se razvija u električnom kolu je:

 

                                                                                                          (13)

 

Proizvod kompleksne efektivne vrijednosti napona i konjugovano kompleksne efektivne vrijednosti struje daje kompleksnu predstavu ukupne snage u kolu, poznate pod nazivom kompleksna snaga:

 

                                                                                                 (14)

 

Dakle, aktivna snaga jednaka je realnom dijelu komplksne snage:

 

                                                                                             (15)

 

dok je reaktivna snaga jednaka imaginarnom dijelu kompleksne snage:

 

                                                                                              (16)

 

Jednačina koja povezuje ukupnu, aktivnu i reaktivnu snagu u nekom električnom kolu jednaka je modulu kompleksne snage:

 

                                                                                                    (17)

 

i naziva se prividna snaga.

 

 

Pitanja za vježbu

 

 

  1. Kako se određuje ukupna otpornost (impedansa) električnog kola u kome su paralelno vezani kondenzator i otpornik?

 

  1. Kako se računa fazna razlika između napona i struje?

 

  1. Šta prednjači: struja ili napon? Zašto?

 

  1. Kako se računa trenutna vrijednost struje u  kolu?

 

  1. Kako se računa trenutna vrijednost struje u pojedinim elementima kola?

 

 

 

Odgovori na pitanja

 

  1. Ukupna impedansa ovakvog kola se određuje prema izrazu:

 

 

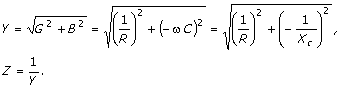
  1. Fazna razlika između napona i struje se računa prema obrascu:

 

 

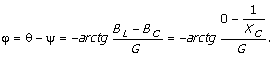
  1. Struja prednjači naponu. Kolo je, kao što se vidi pretežno kapacitivno.

 

  1. Trenutna vrijednost struje u kolu dobije se kad se trenutna vrijednost napona na generatoru podijeli sa ukupnom impedansom kola:

 

 

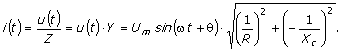
  1. Trenutna vrijednost struje na kondenzatoru se dobije kad se napon na kondenzatoru podijeli s njegovom impedansom (najčešće samo kapacitivnom otpornošću), tj:

 

 

a trenutna vrijednost struje na otporniku se dobije tako što se trenutna vrijednost napona na otporniku podijeli sa njegovom aktivnom otpornosti, dakle: