Primjer 1.
Tanki
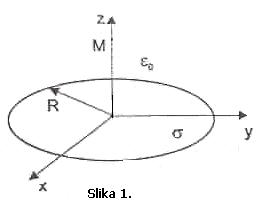
kružni disk poluprečnika R, ravnomjerno naelektrisan gustinom površinskog
naelektrisanja s (s>0), prikazan je na Slici 1. Disk se nalazi u vazduhu. Odrediti:
a)
vektor električnog polja u tački M koja
se nalazi na osi kružnog diska na visini ![]()
b)
potencijal tačke M.
Rješenje:
Vektor
jačine električnog polja u tački M koja se nalazi na visini ![]() od centra kružnog
diska rezultat je djelovanja površinske gustine naelektrisanja s koja je ravnomjerno raspoređena. U ovom slučaju posmatra se vektor jačine
električnog polja
od centra kružnog
diska rezultat je djelovanja površinske gustine naelektrisanja s koja je ravnomjerno raspoređena. U ovom slučaju posmatra se vektor jačine
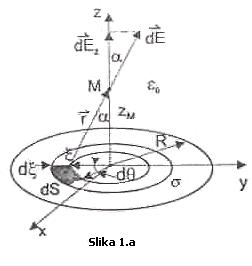
električnog polja ![]() kojeg u tački M
stvara količina naelektrisanja dQ koja se nalazi na elementarnoj
površini dS, što je i prikazano na Slici 1. a.
kojeg u tački M
stvara količina naelektrisanja dQ koja se nalazi na elementarnoj
površini dS, što je i prikazano na Slici 1. a.
Količina naelektrisanja dQ koja se
nalazi na elementarnoj površini dS iznosi:
![]()
gdje je:
![]()
Vektor jačine
električnog polja
![]() u tački M je u pravcu vektora raspojanja
u tački M je u pravcu vektora raspojanja
![]() . Njegov intenzitet određen je sa (ukoliko se smatra da količina naelektrisanja
dQ predstavlja veoma malo "tačkasto" naelektrisanje!):
. Njegov intenzitet određen je sa (ukoliko se smatra da količina naelektrisanja
dQ predstavlja veoma malo "tačkasto" naelektrisanje!):
![]()
Zbog
raspodjele naelektrisanja koja su osno simetrična, moguće je zaključiti da vektori
![]() obrazuju konus sa vrhom u tački M. Analizom se utvrđuje da je
suma projekcija vektora
obrazuju konus sa vrhom u tački M. Analizom se utvrđuje da je
suma projekcija vektora ![]() po x-osi i po y-osi
jednaka nuli:
po x-osi i po y-osi
jednaka nuli:
![]()
![]()
te postoji
samo komponenta ![]() za koju vrijedi:
za koju vrijedi:
![]()
Sa Slike
1.a. intenzitet vektora rastojanja ![]() jednak je:
jednak je:
![]()
i
![]()
odnosno:
![]()
Na osnovu
gornjih jednakosti dobija se intenzitet vektora rezultantne jačine polja u
tački M:
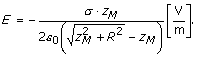
Ukupni
potencijal tačke M je jednak sumi potencijala prozrokovanih količinama
naelektrisanja dQ smještenim na elementarnim površinama dS.
Količina naelektrisanja dQ sa elementarne površine dS stvorit će
potencijal dV u tački M iznosa:
![]()
Ukupni
potencijal koji ima tačka M dobije se kad se djelovanje svih elementarnih
količina naelektrisanja sabere, te je prema tome:
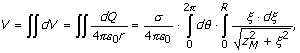
![]()
Primjer 2.
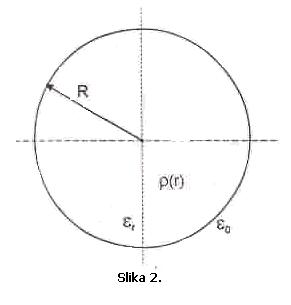
U
unutrašnjosti kugle od materijala relativne dielektrične konstante ![]() , poluprečnika R=0.5 [m] nalazi se raspoređena količina
naelektrisanja čija se gustina zapreminskog naelektrisanja mijenja po zakonu
, poluprečnika R=0.5 [m] nalazi se raspoređena količina
naelektrisanja čija se gustina zapreminskog naelektrisanja mijenja po zakonu ![]() ,
, ![]() što je prikazano na
Slici 2. Izvan kugle je slobodan prostor gdje nema naelektrisanja. Izračuanti
potencijal V u centru kugle.
što je prikazano na
Slici 2. Izvan kugle je slobodan prostor gdje nema naelektrisanja. Izračuanti
potencijal V u centru kugle.
Rješenje:
Potencijal V u centru kugle se određuje kao:
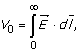
gdje je
tačka referentnog potencijala uzeta u beskonačnosti, jer je kugla konačnog
poluprečnika. Pri kretanju od centra kugle do tačke referentnog potencijala
prolazi se kroz dvije sredine: sredinu sa dielektričnom konstantom ![]() u kojoj postoji
vektor jačine električnog polja
u kojoj postoji
vektor jačine električnog polja ![]() i sredinu sa
dielektričnom konstantom
i sredinu sa
dielektričnom konstantom ![]() u kojoj postoji
vektor jačine električnog polja
u kojoj postoji
vektor jačine električnog polja ![]() .
.
Na osnovu
postojanja dva vektora jačine električnog polja ![]() i
i ![]() , određivanje potencijala u centru kugle se vrši razdvajanjem
integracije na dva dijela:
, određivanje potencijala u centru kugle se vrši razdvajanjem
integracije na dva dijela:
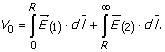
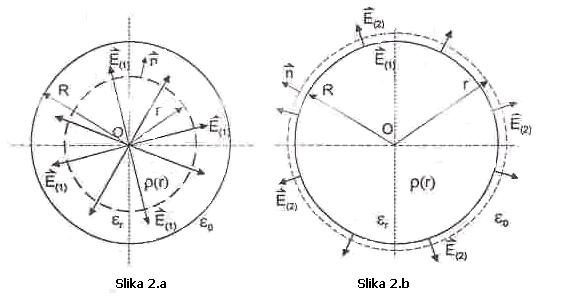
Određivanje
vektora jačine električnog polja ![]() i
i ![]() , vrši se primjenom Gaussove teoreme. Na Slici 2.a. prikazana je zatvorena
površina poluprečnika r (0<r<R), kroz koju se određuje fluks vektora jačine električnog polja
, vrši se primjenom Gaussove teoreme. Na Slici 2.a. prikazana je zatvorena
površina poluprečnika r (0<r<R), kroz koju se određuje fluks vektora jačine električnog polja ![]() .
.
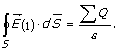
Naelektrisanje
koje je obuhvaćeno zatvorenom površinom poluprečnika r, predstavlja gustinu
zapreminskog naelektrisanja r koja se nalazi u
zapremini unutar zatvorene sfere poluprečnika r:
![]()
S obzirom
da je izvor polja pozitivno naelektrisanje i da je polje radijalno, a da je
normala na zatvorenu površinu usmjerena ka vanjskom prostoru onda je ugao koji
zatvaraju vektor jačine polja ![]() i vektor normale
i vektor normale ![]() jednak 0. Na osnovu toga
je:
jednak 0. Na osnovu toga
je:
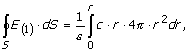
![]()
![]()
Na Slici
2.b. prikazana je zatvorena površina poluprečnika r (r>R), kroz koju se
određuje fluks vektora jačine električnog polja ![]() .
.
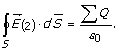
Naelektrisanje
koje je obuhvaćeno zatvorenom površinom poluprečnika r predstavlja gustinu
zapreminskog naelektrisanja r koja se nalazi u
zapremini unutar kugle poluprečnika R.
I u ovom
slučaju, ugao koji stvaraju vektor jačine električnog polja ![]() i vektor normale
i vektor normale ![]() jednak je 0. Na
osnovu toga vektor jačine električnog polja
jednak je 0. Na
osnovu toga vektor jačine električnog polja ![]() određuje se kao:
određuje se kao:
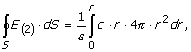
![]()
![]()
Uz
definirane vektore ![]() i
i ![]() , i uz uslov da vektori
, i uz uslov da vektori ![]() i
i ![]() jednaki određuje se
potencijal u centru kugle:
jednaki određuje se
potencijal u centru kugle:
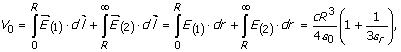
![]()
Primjer 3.
Nacrtati i objasniti sliku polja za
slučaj nenaelektrisanog provodnog loptastog tijela sa šupljinom u koju je
unijeto pozitivno tačkasto naelektrisanje Q postavljeno u centar.
Rješenje:
Ekranizirajuće dejstvo šupljih
provodnih tijela postoji samo u slučaju polja koja potiču od vanjskih
naelektrisanja. Kada se u unutrašnjost nekog šupljeg nenaelektrisanog provodnog
tijela unese tačkasto naelektrisanje Q, zbog pojave električne indukcije na
unutrašnjem zidu lopte indukovat će se naelektrisanje suprotnog znaka od znaka
naelektrisanja Q. Pošto je uslovom zadatka unijeto pozitivno tačkasto
naelektrisanje, to će se na unutrašnjoj površini pojaviti indukovano
naelektrisanje – Q, a na vanjskoj površini +Q.
Pojava
negativnih indukovanih naelektrisanja na unutrašnjoj površini je posjedica
privlačnog dejstva unesenog pozitivnog naelektrisanja Q na elektrone u zidu
tijela. Ova indukovana nalektrisanja na unutrašnjem zidu tako su raspoređena da
zajedno sa unesenim naelektrisanjem Q obezbjede uslov da u unutrašnjosti da u
unutzrašnjosti provodnog zida vektor jačine električnog polja E bude jednak
nuli (Slika 3.).
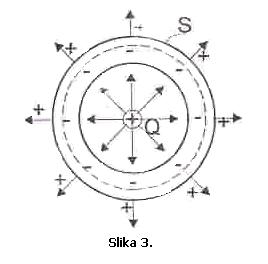
Primjenjujući
Gaussov zakon na zamišljenu zatvorenu površinu S unutar provodnog zida fluks vektora E kroz površ S je 0, jer u svim
tačkama zatvorene površine E=0. to znači da je ukupno obuhvaćeno naelektrisanje
jednako nuli. Ako je
![]() ukupno indukovano naelektrisanje na
unutrašnjem zidu lopte, onda je primjenom Gaussovog zakona i gornjeg zaključka,
ukupno naelektrisanje jednako:
ukupno indukovano naelektrisanje na
unutrašnjem zidu lopte, onda je primjenom Gaussovog zakona i gornjeg zaključka,
ukupno naelektrisanje jednako:
![]()
odnosno:
![]()
Uslovom
zadatka šuplja lopta je nenaelektrisana, što znači da će se na vanjskoj
površini lopte indukovati pozitivno naelektrisanje +Q.
Jačina
polja u zidu jednaka je nuli, unutrašnja naelektrisanja +Q (tačkasto uneseno) i
indukovano naelektrisanje na unutrašnjoj površini zida –Q, nemaju nikakvog
uticaja na raspodjelu naelektrisanja na vanjskoj površini lopte. Ova raspodjela
jedino zavisi od oblika vanjske površine tijela. S obzirom da je šuplje provodno
tijelo lopta, to će raspodjela površinskog naelektrisanja biti ravnomjerna.
Kako
potencijal naelektrisanja Q (za referentnu tačku u beskonačnosti) iznosi:
![]()
to su
linije polja radijalni zraci. Ekvipotencijalne površi su koncetrične sfere.
Kakva je
raspodjela indukovanih naelektrisanja u nenaelektrisanoj provodnoj lopti kada
je tačkasto naelektrisanje postavljeno van centra lopte?
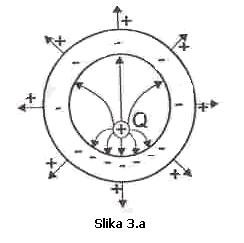
U slučaju
da tačkasto naelektrisanje Q nije postavljeno u centru lopte ukupno indukovano
naelektrisanje na unutrašnjem zidu lopte je –Q i može se provesti ista analiza.
Raspodjela indukovanih naelektrisanja prikazana je na Slici 3.a.
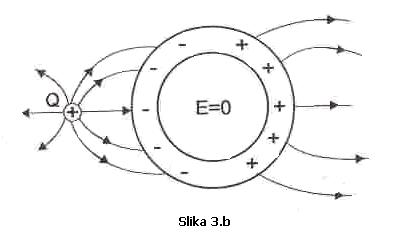
Na kraju, može se analizirati slučaj
kada je u blizini šuplje provodne lopte, sa njene vanjske strane, postavljeno
naelektrisanje +Q, Slika 3. b.
Primjer 4.
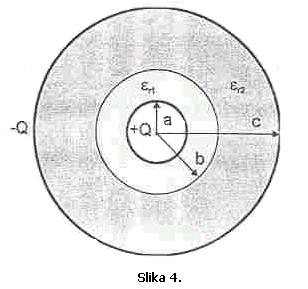
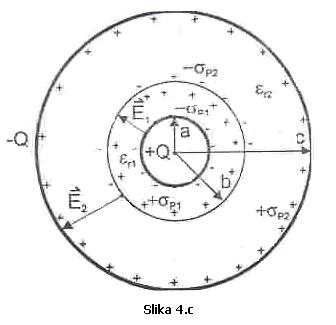
Na Slici 4. prikazan je sferni
kondenzator, unutrašnje elektrode poluprečnika a na kojoj se nalazi naelektrisanje Q (Q>0). Između elektroda
kondenzatora su dva koncetrična sloja dielektrika relativnih dielektričnih
konstanti ![]() i
i ![]() . Poluprečnik granične sferne površine između ova dva
dielektrika je b, a poluprečnik spoljašnje elektrode je c.
. Poluprečnik granične sferne površine između ova dva
dielektrika je b, a poluprečnik spoljašnje elektrode je c.
Odrediti:
a)
vektore jačine
električnog polja, električnog pomjeraja i električne polarizacije
b)
gustine površinskih vezanih
naelektrisanja
c)
izraz za potencijal tačaka između
elektroda uzimajući da se spoljašnja elektroda nalazi na nultom potencijalu
d)
kapacitet kondenzatora
Rješenje:
Sistem od dvije koncentrične međusobno izolirane metalne
sfere, čije je međusobno rastojanje malo u odnosu na prečnik spoljašnje metalne
sfere predstavlja sferni kondezator.
Unutar
kondezatora postoje dva vektora jačine električnog polja ![]() i
i ![]() , u sredini relativnih dielektričnih konstanti
, u sredini relativnih dielektričnih konstanti ![]() i
i ![]() , respektivno, kao i dva vektora električnog pomjeraja
, respektivno, kao i dva vektora električnog pomjeraja ![]() i
i ![]() . U unutrašnjosti sfernog kondezatora električno polje je
radijalno. Vektor jačine elelktričnog polja i električnog pomjeraja su normalni
na graničnu površ, tako da se može primjeniti sljedeći granični uslov:
. U unutrašnjosti sfernog kondezatora električno polje je
radijalno. Vektor jačine elelktričnog polja i električnog pomjeraja su normalni
na graničnu površ, tako da se može primjeniti sljedeći granični uslov:
![]()
Vektor jačine električnog polja u
kondenzatoru postoji samo u prostoru između dvije elektrode, odnosno u dijelu
gdje je a>r>c.
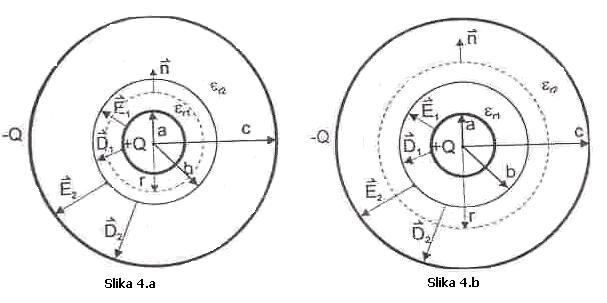
Vektor
električnog pomjeraja određuje se primjenom Maxwellovog postulata na sfernu
površinu poluprečnika r, koja se nalazi u prostoru između lopti i koncentrična
je sa elektrodama. Na slikama prikazane su sfere (isprekidana linija) na koje
se primjenjuje Maxwellov postulat za određivanje vektora električnog pomjeraja ![]() i
i ![]()
![]() za a<r<c.
za a<r<c.
Vektor
električnog pomjeraja je kolinearan sa vektorom normale ![]() na zatvorenu
površinu, a količina naelektrisanja koja je obuhvaćena ovom sferom je
naelektrisanje unutrašnje elektrode Q, tako da električni pomjeraj D iznosi:
na zatvorenu
površinu, a količina naelektrisanja koja je obuhvaćena ovom sferom je
naelektrisanje unutrašnje elektrode Q, tako da električni pomjeraj D iznosi:
![]()
Intenzitet
vektora jačine električnog polja ![]() iznosi:
iznosi:
![]() za a<r<b,
za a<r<b,
a unutar
dielektrika relativne dielektrične konstante ![]() , intenzitet vektora jačine električnog polja
, intenzitet vektora jačine električnog polja ![]() je:
je:
![]() za b<r<c.
za b<r<c.
Unutar
dielektrika relativne dielektrične konstante ![]() , intenzitet vektora električne polarizacije
, intenzitet vektora električne polarizacije ![]() iznosi:
iznosi:
![]() za a<r<b,
za a<r<b,
a unutar
dielektrika relativne dielektrične konstante ![]() , intenzitet vektora električne polarizacije
, intenzitet vektora električne polarizacije ![]() iznosi:
iznosi:
![]() za b<r<c.
za b<r<c.
Gustine
površinskih vezanih naelektrisanja brojno su jednake intenzitetima vektora
polarizacije. U dielektriku relativne dielektrične konstante ![]() određuje se gustina površinskih vezanih naelektrisanja
određuje se gustina površinskih vezanih naelektrisanja ![]() a u dielektriku
relativne dielektrične konstante
a u dielektriku
relativne dielektrične konstante ![]() određuje se gustina površinskih vezanih naelketrisanja
određuje se gustina površinskih vezanih naelketrisanja ![]() Zbog sfernog oblika
kondenzatora intenziteti gustina površinskih vezanih naelektrisanja
Zbog sfernog oblika
kondenzatora intenziteti gustina površinskih vezanih naelektrisanja ![]() i
i ![]() , unutar jednog dielektrika nisu isti,
, unutar jednog dielektrika nisu isti, ![]() odnosno
odnosno ![]() pa je:
pa je:
![]()
Zbog postojanja dva dielektrika između
elektroda sfernog kondenzatora, odnosno postojanja dva vektora jačine
električnog polja izraz za potenciijal tačaka između elektroda moguće je
odrediti za dva slučaja:
Prvi slučaj:
Tačke za
koje se određuje potencijal nalaze se unutar dielektrika relativne dielektrične
konstante ![]() , odnosno za b<r<c tada je:
, odnosno za b<r<c tada je:
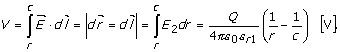
Drugi slučaj:
Tačke za
koje se određuje potencijal, nalaze se unutar dielektrika relativne
dielektrične konstante ![]() , odnosno a<r<b tada je:
, odnosno a<r<b tada je:
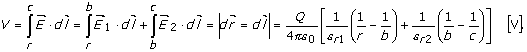
Da bi se
odredio kapacitet ovog sfernog kondenzatora neophodno je odrediti napon na
elektrodama kondenzatora:
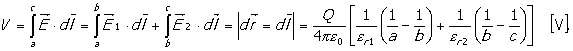
Kapacitet
kondenzatora iznosi:
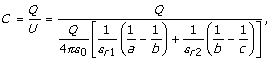
![]()
Primjer 5.
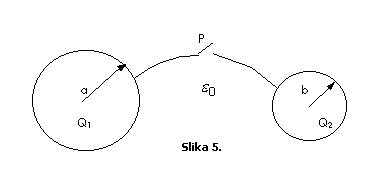
U vazduhu
se nalaze dvije provodne sfere poluprečnika a i b, kao na Slici 5.
Naelektrisanja sfera iznose ![]() i
i ![]() . Odrediti energiju polja sfera prije i poslije zatvaranja
prekidača P.
. Odrediti energiju polja sfera prije i poslije zatvaranja
prekidača P.
Rješenje:
Pri
otvorenom prekidaču P potencijali sfera su:
![]()
![]()
Energija
polja sistema dva naelektrisana tijela količinama naelektrisanja ![]() i
i ![]() koja se nalaze na
potencijalima
koja se nalaze na
potencijalima ![]() i
i ![]() se može računati kao:
se može računati kao:
![]()
odnosno za
dati slučaj:
![]()
Poslije
zatvaranja prekidača P sfere će biti na istom potencijalu, a ukupno
naelektrisanje sfera se neće promijeniti. Dakle, vrijedi:
![]()
![]()
Rješenjem
ovog sistema jednačina dobiju se iznosi naelektrisanja koja se nalaze na
sferama nakon zatvaranja prekidača:
![]()
![]()
Potencijal
na obje sfere je:
![]()
Energija
polja sfera nakon zatvaranja prekidača je:
![]()